Le jardinier numérique (3/4): interprétation graphique

Nous pouvons interpréter graphiquement un L-système en utilisant une tortue (celle que l'on trouve par exemple dans LOGO➶) à qui l'on commande ses déplacements en fonction des lettres du mot considéré. Cette interprétation a été proposée pour la première fois par Szilard et Quinton en 1979 (An interpretation for DOL systems by computer graphics).

L'état de la tortue est défini par un triplet $(x, y, \alpha)$ où $(x, y)$ sont les coordonnées cartésiennes de la tortue dans le plan, et l'angle $\alpha$ est la direction dans laquelle regarde la tortue.

En fixant la longueur $d$ d'un pas de tortue et une incrémentation d'angle $a$ , on peut commander la tortue avec des ordres représentés par les symboles suivants (ces symboles constituent l'alphabet de nos L-systèmes) :

F : avancer en avant d'un pas en dessinant.
f : avancer en avant d'un pas sans dessiner.
+ : tourner à gauche d'un angle $a$ .
- : tourner à droite d'un angle $a$ .

Quand la tortue avance, son état change en $(x', y', \alpha)$ où $x' = x + d\cos\alpha$ et $y' = y + d\sin\alpha$ . Quand la tortue tourne, son état change en $(x, y, \alpha \pm a)$ .

Dessiner à l'écran

Avant de dessiner une quelconque plante ou même de traduire les symboles précédents en instruction pour tortue, il nous faut déjà savoir dessiner à l'écran. Pour cela, bien sûr, je vais choisir comme langage de programmation Scheme (plus spécifiquement Guile➶), et nous utiliserons le module turtle que j'ai créé et qui présente l'avantage de disposer d'une tortue capable de dessiner.

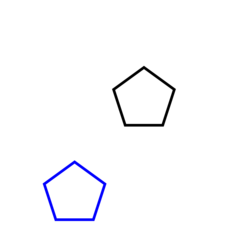
Pour nous exercer, nous allons suivre le tutoriel du module turtle que nous adapterons afin de dessiner deux pentagones de couleurs différentes.

#! /usr/bin/guile -s
!#

;; add the directory that is in the load path
(add-to-load-path (dirname (current-filename)))

;; access turtle public interface
(use-modules (turtle))

;; instructions to draw a pentagon side
(define (side x) (list (forward x) (turn-left 72)))

;; instructions to draw a pentagon by repeating a side
(define (pentagon x) (repeat 5 (side x)))

;; instructions to move and change color
(define (move)
  (list (pen-up) (turn-right 144) (forward 50) (color 0 0 255) (pen-down)))

;; instructions to draw 2 pentagons at 2 locations with 2 colors
(define (two-pentagons x)
  (append (pentagon x) (move) (pentagon x)))

;; draw 2 pentagons whose sides are 30 pixels long
(draw (two-pentagons 30))

Deux pentagones : l'un bleu, l'autre noir

Traduire des symboles en instructions pour tortue

Maintenant que nous savons dessiner et contrôler notre tortue, nous souhaitons qu'elle comprenne les symboles F, f, + ou -. Pour cela, nous allons créer une fonction translate-symbol qui prend en entrée un symbole et nous retourne une liste d'instructions compréhensibles par la tortue. Et puisque nous voulons non pas traduire un symbole à la fois, mais des mots entiers en une liste d'instructions, nous allons également créer une fonction translate-word. Le but étant de dessiner le mot +FfF-FF-F-F+F+FF-F-FFF.

#! /usr/bin/guile -s
!#

(add-to-load-path (dirname (current-filename)))
(use-modules (ice-9 match) (turtle))

;; translate a symbol into a list of instructions
(define (translate-symbol length angle symbol)
  (match symbol
    ('F (list (pen-down) (forward length)))
    ('f (list (pen-up) (forward length)))
    ('+ (list (turn-left angle)))
    ('- (list (turn-right angle)))))

;; translate a word of symbols into a list of instructions
(define (translate-word length angle word)
  (define (iter remaining-symbols instructions)
    (if (null? remaining-symbols)
        instructions
        (iter (cdr remaining-symbols)
              (append instructions
                (translate-symbol length angle (car remaining-symbols))))))
  (iter word '()))

;; define a word as a list of symbols
(define word '(+ F f F - F F - F - F + F + F F - F - F F F))

;; translate the word into instructions
(define instructions (translate-word 40 90 word))

;; follow the instructions to draw an image
(draw instructions)

Dessiner des fractales

Nous sommes désormais capables de faire correspondre une image à un mot. Il nous faut maintenant générer des L-systèmes qui nous fournirons des mots à dessiner. Pour cela, nous allons créer une fonction transform-symbol qui à partir d'un symbole de notre alphabet et d'un ensemble de productions va nous donner la transformation à appliquer. Et puisque nous souhaitons transformer des mots entiers, nous créerons également la fonction transform-word qui transformera un mot en un autre en fonction du nombre d'itérations voulues.

Nous allons commencer par dessiner le L-système suivant :

$\omega = F - F - F - F$
$P = \{ (F \rightarrow F - F + F + F F - F - F + F) \}$

Avec les paramètres suivants :

itérations = 3
longueur d = 4
angle a = 90°

...

;; transform a symbol into its successor in the set of productions
(define (transform-symbol symbol productions)
  (if (null? productions)
      (list symbol)
      (if (equal? symbol (caar productions))
          (cadar productions)
          (transform-symbol symbol (cdr productions)))))

;; tranform a word into another by applying productions n times
(define (generate-word n word productions)
  (define (iter n word generated-word)
    (if (null? word)
        (iter (- n 1) generated-word '())
        (if (= n 0)
            word
            (iter n
                  (cdr word)
                  (append generated-word
                    (transform-symbol (car word) productions))))))
  (iter n word '()))

;; generate a word
(define word
  (generate-word 3 '(F - F - F - F) '((F (F - F + F + F F - F - F + F)))))

;; translate the word into instructions
(define instructions (translate-word 4 90 word))

;; follow the instructions to draw an image
(draw instructions)

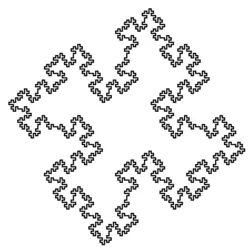
Île de Minkowski (3 itérations)

L'exemple précédent révèle la relation étroite entre les L-systèmes et les courbes de Koch (des courbes fractales). Il est aisé de modifier des L-systèmes pour obtenir de nouvelles courbes de Koch en ajoutant, retirant ou modifiant certains symboles de l'axiome ou des productions. Partons du même axiome $\omega = F - F - F - F$ et modifions les règles de productions pour observer leurs impacts.

S'obtient avec le L-système suivant :

$\omega = F - F - F - F$
$P = \{ (F \rightarrow F F - F - F - F - F - F + F) \}$

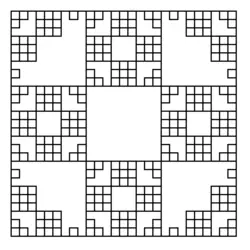
S'obtient avec le L-système suivant :

$\omega = F - F - F - F$
$P = \{ (F \rightarrow F F - F - F - F - F - F + F) \}$

Nous pouvons ainsi obtenir une variété de courbes en modifiant simplement les règles de production de nos L-systèmes.

Création de DOL-systèmes

Il est intéressant de construire des L-systèmes dont la structure graphique est celle issue d'un processus de développement. Ce problème, nommé problème d'inférence, n'est à ce jour pas résolu efficacement par des algorithmes. Des méthodes heuristiques qui s'appuient sur les interprétations graphiques des L-systèmes existent :

la réécriture des arêtes,
la réécriture des nœuds.

Dans le cas de la réécriture des arêtes, les productions remplacent les arêtes par des figures. Tandis que dans la réécriture des nœuds, les productions remplacent les sommets entre les arêtes par des figures. Nous n'entrerons pas ici dans les détails de la création pratique de tels systèmes, mais il est à noter que les types de courbes générées en utilisant ces techniques de réécriture ne sont pas disjoints.

D'ailleurs, un exemple de courbe obtenu avec ces techniques de réécriture est la courbe du dragon. Tentons de la dessiner grâce au L-système suivant :

$\omega = F l$
$P = \{ (l \rightarrow l + r F +), (r \rightarrow - F l - r) \}$

Avec les paramètres suivants :

itérations = 12
longueur d = 4
angle a = 90°

Nous remarquons la présence de nouveaux symboles dans notre alphabet (l et r). Ceux-ci sont utilisés uniquement dans le processus de réécriture , ils n'ont pas pour objectif de donner une instruction à la tortue. On va donc légèrement modifier notre fonction de traduction translate-symbol afin que la tortue ne bouge pas lorsqu'elle rencontre l ou r.

En fait, les symboles l pour left (gauche) et r pour right (droite) servent à distinguer deux types d’arêtes dans le graphe : celles qui partent à gauche et celles qui partent à droite. Cela permet d’appliquer des règles différentes selon le côté, et donc de faire évoluer la structure de manière plus précise à chaque itération du L-système. L’introduction de l et r permet ainsi de mieux contrôler la forme finale du graphe, en tenant compte de l'organisation spatiale, et c'est là un aspect important lorsqu’on cherche à modéliser des structures biologiques.

...

;; translate a symbol into a list of instructions
(define-public (translate-symbol length angle symbol)
  (match symbol
    ('F (list (pen-down) (forward length)))
    ('f (list (pen-up) (forward length)))
    ('+ (list (turn-left angle)))
    ('- (list (turn-right angle)))
    ;; no particular action performed by the turtle
    ('l '())
    ('r '())))

...

;; generate a word
(define word
  (generate-word 12 '(F l) '((l (l + r F +)) (r (- F l - r)))))

;; translate the word into instructions
(define instructions (translate-word 4 90 word))

;; follow the instructions to draw an image
(draw instructions)

Et voici le résultat :

Un dragon (12 itérations)

Encore un peu et nous serons capables de dessiner nos premières plantes.

Suite de la promenande botanique